晨跑时用抛硬币决定路线,分组时靠抛硬币定顺序——“抛硬币”早成了我们眼中最公平的“随机工具”。可若开个脑洞:把抛硬币的10秒钟精准复刻,手指发力、空气流动甚至灰尘位置都分毫不差,硬币落地还会有意外吗?这个问题看似天马行空,却藏着一个直击科学认知的悖论。
一、搭建“零变量”的时间重复舞台
要让这个悖论成立,核心前提是绝对无差别的时间复刻。这不是简单的“再来一次”,而是像电脑复制文件般的精准还原:第一次抛硬币时,你用拇指和食指捏在硬币边缘1/3处,向上发力0.5牛顿,硬币以每秒15圈的速度旋转,在空中划过20厘米弧线后落在3.5硬度的水泥地;重复时刻,你的动作、空气气流、地面硬度甚至周围尘埃位置都完全重叠,没有任何变量窜入。
按中学物理课的力学规律,结果其实早已注定。就像小球从同一高度滚落必然沿同一路径运动,初始条件完全相同的硬币,运动轨迹会精准重叠——第一次是正面,之后每一次复刻都只会是正面。
二、矛盾爆发:“随机”为何突然消失?
可我们从小就被灌输“抛硬币是典型随机事件”:数学老师说它正面概率50%,游戏时我们靠它“听天由命”,其核心魅力正在于“不确定性”。但在“时间完美重复”的假设里,这份“不确定”凭空消失了:硬币结果被物理规律死死锁定,没有丝毫意外可能。
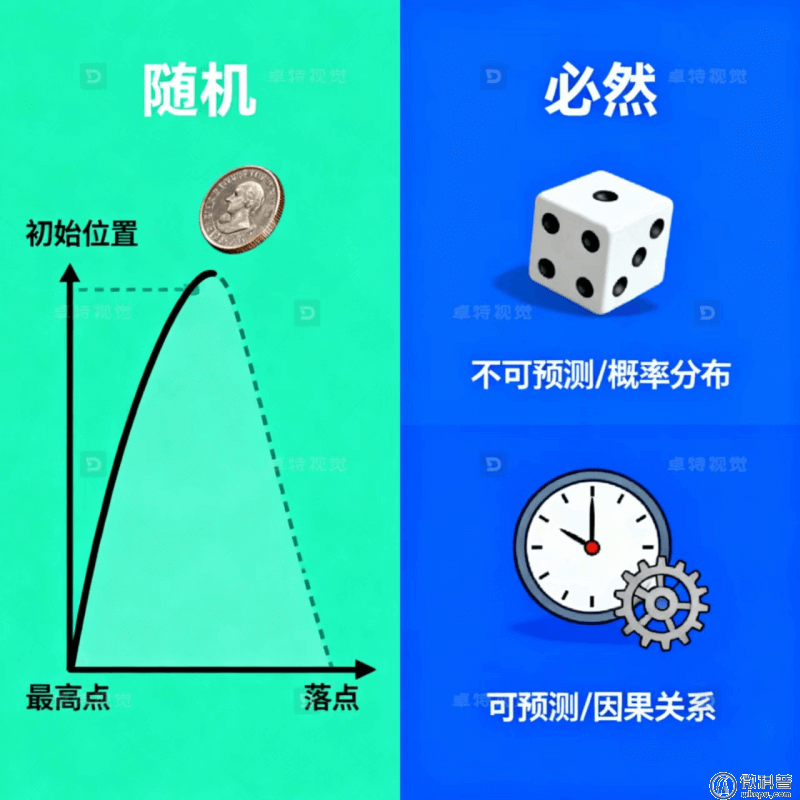
两个看似都对的结论就此碰撞:
- 物理规律层面:完美重复=结果必然(永远同一面);
- 普遍认知层面:抛硬币=随机事件(结果不确定)。
这种冲突,本质上是“科学规律”与“日常经验”的正面相遇。
三、悖论背后:随机的本质是“力所不及”?
这个矛盾之所以耐人寻味,是因为它戳中了一个底层问题:我们说的“随机”,是事件本身不确定,还是我们没能力掌控所有变量?
现实中抛硬币的“随机感”,其实源于人类的“掌控局限”:我们无法精确控制手指发力的细微差异,没法预判气流的瞬间变化,更算不清硬币与空气的摩擦系数——这些“失控变量”让结果变得不可测。但就像“时间重复”假设中那样,一旦消除所有变量,“随机”便会消失,剩下的只有物理规律决定的“必然”。
这和我们熟悉的游戏抽卡异曲同工:玩家觉得“抽到SSR全凭运气”,但在程序员眼中,结果早由“随机数算法”与账号ID绑定,只要掌握这些“隐藏变量”,结果完全可预测。我们的悖论不过是把这点放大:当所有变量被“冻结”,“随机”或许只是人类对“力所不及”的妥协。
四、脑洞的价值:在假设中锻炼科学思维
有人可能会说“时间根本无法重复,想这些没用”。但科学探索往往始于看似无用的假设:从“如果地球是圆的”到“如果光速不变”,许多重大突破都源于对“不可能”的追问。

这个悖论的意义,正在于帮我们跳出经验误区。就像古人曾认为“打雷闪电是随机的”,直到后来才知晓其是云层电荷的必然反应。今天我们眼中的“随机”,或许只是尚未破解的“必然”。下次再抛硬币时,若能想到“眼前的50%概率,其实是一堆没搞懂的变量”,便已触摸到科学思维的核心——不盲从经验,多追问“为什么”。
对大学生而言,这种“悖论式思考”更是宝贵的能力。无论是专业课上的实验设计,还是科研中的问题拆解,本质上都是在寻找那些“隐藏变量”,让“不确定”变得“可掌控”。而这个关于硬币与时间的脑洞,正是锻炼这种思维的绝佳载体。从这个角度看,“随机”从来都不是事件本身的属性,而是人类认知和操控能力边界下的产物。无论是抛硬币还是抽卡,当我们能掌握所有初始条件和运行规律,所谓的“不确定性”就会彻底瓦解,剩下的只有可预测的必然。这一悖论也让我们明白,科学思维的核心之一,就是分清“客观规律的必然性”和“主观认知的局限性”,不把自身能力的边界当成事物本身的边界,而这个就象征了随机现象的底层逻辑。
本文作者:新疆大学计算机科学与技术学院信息安全专业 陈果。
责编:微科普